Compare different attribution models on a simulated traffic allocation problem based on real customer journeys

The algorithm compares 5 attribution methodologies: first touch, last touch, linear touch, Markov model, Shapley value and Logistic regression in a traffic allocation problem based on real data.

1. Consider a set of customer journeys on a time range. This set will be called the population

PATH	CONVERSIONS	NULLS
A > C > A > B	2	125
B > C	3	78
D	1	0
...	...	...

2. Calculate population conversion rate

$pcr=\frac{\sum_{paths} Conversions}{\sum_{paths} Conversions + \sum_{paths} Nulls}$

3. If flg_extra_path = 1, for each distinct path, add a number of nulls proportional to the population conversion rate

PATH	CONVERSIONS	NULLS
A > C > A > B	2	125 + int(1/pcr)
B > C	3	78 + int(1/pcr)
D	1	0 + int(1/pcr)
...	...	...

This step of data augmentation ensures that no trivial solution can be found to the allocation problem. Without data augmentation would be trivial to allocate all the traffic to D, because D has a conversion rate equal to 1. But this is unrealistic because D is included in only one path and no valid statistical consideration can be done on its conversion rate.

4. Generate a random sample from the population. The length of the sample is given by:

max(perc_sample*len(population), max_nsim)

5. For the random sample, count the traffic on each channel (traffic = the number of touchpoints for a channel)

CHANNEL	TRAFFIC
A	1450
B	2340
C	450

6. For each Model, for each Channel calculate an importance weight

FIRST TOUCH, LAST TOUCH, LINEAR TOUCH

weight[X] = Attribution[X] / Sum Conversions For each X, where X is a generic channel

MARKOV MODEL, SHAPLEY VALUE

weight[X] = Odds(X) / Sum Odds(X) For each X, where X is a generic channel

7. For each Model, for each Channel, allocate traffic using the following formula:

traffic_new[X]=

(1 - min_perc_traffic - perc_reall) * traffic[X] + (min_perc_traffic / number_of_channels * total_traffic) + (weight[X]/total_weight*perc_reall * total_traffic)

For each X, where X is a generic channel

8. For each Model generate a random sample of customer journeys from the population given the allocated traffic. It means that each time I sample a customer journey the available traffic on each channel has to be decreased. So if the available traffic for each channel is

A -> 120
B -> 50
C -> 40

And I sample:

A > A > B > (NULL)

Then the available traffic becomes:

A -> 118
B -> 49
C -> 40

Continue to sample random customer journeys until the available traffic is terminated.

9. For each Model, calculate the conversion rate on the random sample at point .6

10. Repeat 4-9 niter times and store each time the conversion rates

Considerations

1. The algorithm allocates traffic and not budget, implicitly assuming that there is a linear relationship between budget and traffic.

2. The algorithm also implicitly assumes a linear relationship between the traffic on a channel and the number of conversions that this channel can generate.

3. The algorithm considers as input real customer journeys but the customer generation mechanism does not incorporate all the complexity and non-linearity of a real problem.

These considerations limit the application of the algorithm to small variations of the previously allocated budget. Because for small variations, assuming linearity does not invalidate the results of the analysis. Thus perc_reall should be around 10%.

So if a small variation of the budget is the goal, this procedure is able to rank the Models for their ability to direct traffic to the most converting customer journeys.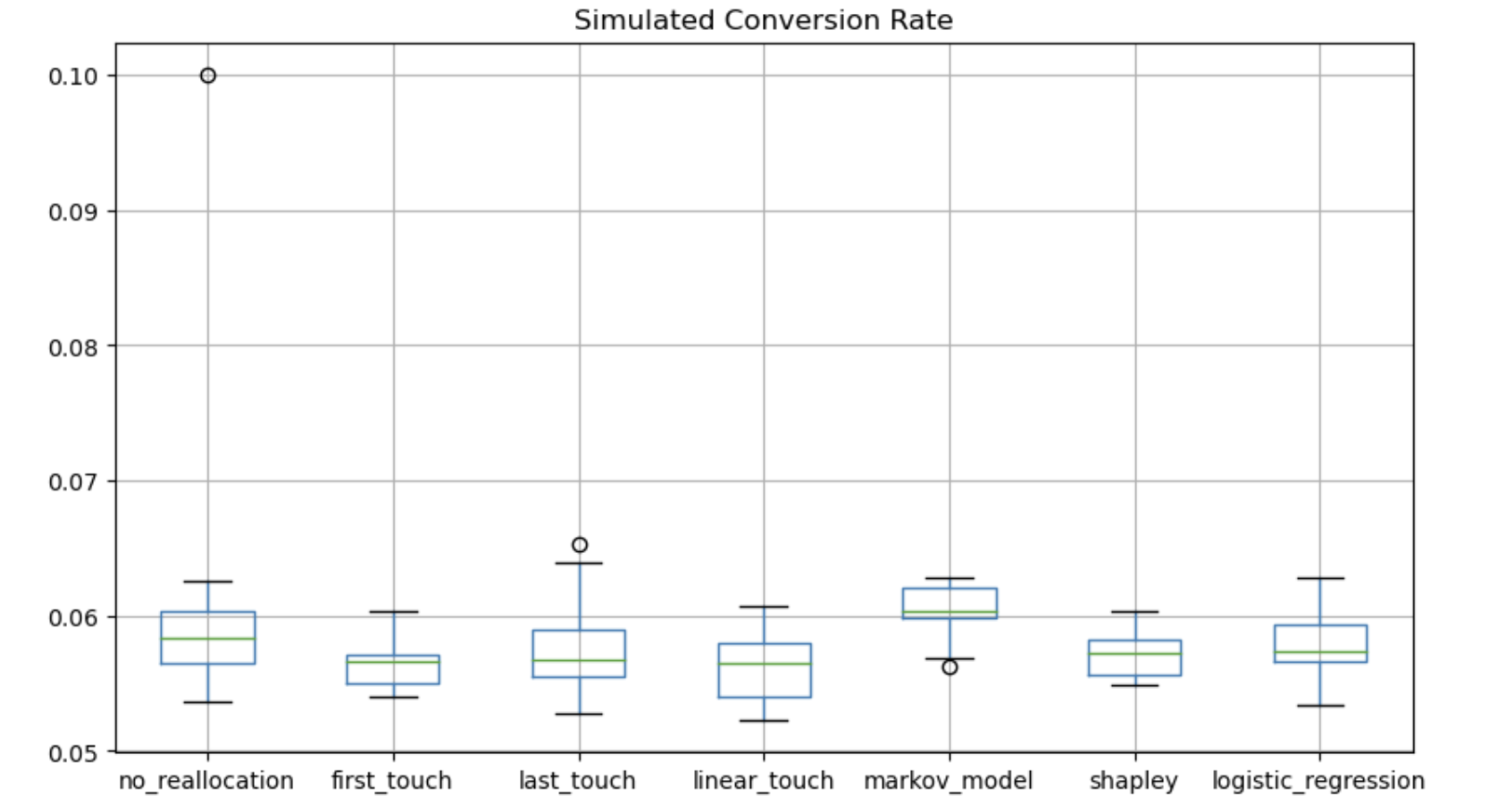

The output of the procedure is the simulated conversion rates for each Channel which are in general larger than the population conversion rate. That's because of the linearity assumptions. Thus the methodology is useful for ranking the Models but it does not give information about how much conversion rate one can gain by applying a Model with respect to another Model. So, if we look at the plot above, it's not correct to say that by applying Markov model one can reach a 6% conversion rate. But it's correct to say that Markov model is the model that shows the better ability to direct traffic to the most converting customer journeys.